几何研究的就是点、线、面、体,点构成线,线构成面和角,面构成体。
经过两点有且只有一条直线,两点确定一条直线
以一个端点做直线,叫做射线
连接两个端点的直线叫做线段
两点之间线段最短,也叫做两点间距离
把线段分成两等份的点叫做线段的中点
初中阶段,使用无刻度的直尺和圆规作图叫做尺规作图
(1) 长度的单位
国际单位:
千米(公里)、米、厘米、毫米、微米、纳米
各国的内部长度单位
英国的英尺,英里,中国的市尺、里。
(2) 长度的测量工具
直尺、卷尺、游标卡尺等,测量精度需求不高时,可以用步、肘、拃等来估算距离
(3) 测量方法
两条直线有一个公共点,叫做两直线相交,公共点叫做交点
两条直线相交形成角,角由顶点和两条边构成。
角度的单位:度、分、秒,符号分别记作:º、"、′。
1度角记作1º,
1度=60分 1分=60秒
一周角=360º,平角=180º,直角=90º

此外角的单位还有弧度、密位
测量角的工具有:量角器、经纬仪等
1)通过角度度量工具直接测量并比较
2) 一条边和顶点重合,比较另一边的位置比较大小
1) 按照角的大小分类
锐角、直角、钝角、平角、周角
2) 按照相互关系
余角:两角之和为90度,则两角互为余角,同角或者等角的余角相等。
补角:两角之和为180度,则两角互为补角,同角或者等角的补角相等。
邻补角:两角有一个公共边,另一边互为反向延长线,这两个叫做互为邻补角,互为邻补角的两角之和为180度。
对顶角:一个角的两边是另一个角的两边的反向延长线,具有这种位置关系的两个角互为对顶角。
对顶角相等。
3) 相互位置
一条直线与另外两条直线相交,形成很多角,按照他们所在的位置可分类如下:
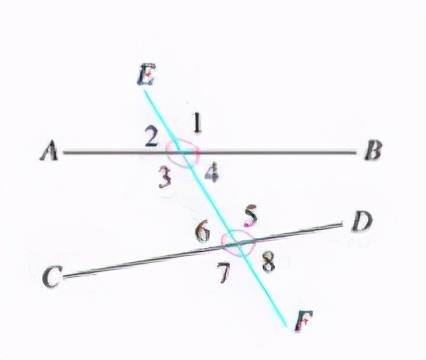
同位角:
∠1和∠5,互为同位角,都在直线 EF的右侧,∠1在直线AB的上方,∠5在直线CD的上方,也就是说他们的位置相同。同理∠4和∠8,∠2和∠6都为同位角,还可以找出那些同位角?
内错角:
∠4和∠6,在直线AB和CD的内侧,分别在EF的两侧,这样的一对角叫做内错角,同理∠3和∠5也为内错角。
同旁内角:
∠4和∠5,都在直线AB和CD的内侧,都在直线EF的同一侧,这样的一对角叫做同旁内角。∠3和∠6也是同旁内角。
1) 角的平分线
从一个角的顶点出发,把这个角为两个相等的角的射线叫做角的平分线
2) 角平分线的性质
角平分线到这个角的两边的距离相等
1) 垂线的定义
两条直线相交,四个角都为直角时这两条直线互相垂直,一条直线叫做另一条直线的垂线,他们的交点叫做垂足。
2) 点与垂线
在同一平面内,过一点有且只有一条直线与已知直线垂直
3) 点到直线的距离
连接直线外一点与直线上各点的所有线段中,垂线段最短,直线外一点到这条直线的垂线段的长度叫做点到直线的距离。
1) 垂直平分线
与线段两个端点距离相等的点在这条线段的垂直平分线上
2) 垂直平分线的性质
线段垂直平分线上的点与这条直线两个端点的距离相等
(3) 轴对称图形
轴对称图形的对称点的连线,被对称轴垂直平分
直线不相交,就叫做平行
1) 直线外一点有且只有一条直线与已知直线平行
2) 如果两条直线都与第三条直线平行,那么这两条直线也互相平行
1) 同位角相等,两直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
2) 内错角相等,两直线平行
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
3) 同旁内角互补,两直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
1)、 平行的定义
2)、 平行公理2
3)、 同位角相等
4)、 内错角相等,、
5)、 同旁内角互补
两条平行线被第三条直线所截,同位角相等。
两条平行线被第三条直线所截,内错角相等。
两条平行线被第三条直线所截,同旁内角互补。







