最近,我发现一些小学六年级的学生在学习圆柱、圆锥的内容时,对于其中的难点问题掌握的不太好,如:圆柱表面积与体积、卷纸问题、容浸问题等。今天我就先为大家详细讲解一下圆柱表面积与体积的知识点。


【例题1】
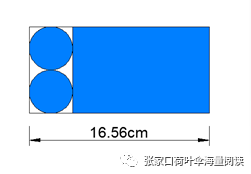
如图,将一块长方形铁皮,利用图中阴影的部分,刚好制成一个油桶,求这个油桶的表面积和体积?
【解题思路】
在图中的已知条件只有长方形的长16.56cm,没有长方形的宽,也没有圆的半径,但是通过观察可以发现长方形的宽就是两个圆直径的和;题中又说“刚好制成一个油桶”说明图中蓝色长方形的长应该等于圆的周长。
公式:2r+2πr=16.56 可以求出r=2cm
油桶的表面积=2×(3.14×2×2)+(2×3.14×2)×(2×4)
=25.12+100.48
=125.6平方厘米
或
油桶的表面积=2×3.14×2×(2+2×4)
=12.56×10
=125.6平方厘米
油桶的体积=(3.14×2×2)×(2×4)
=100.48立方厘米
【例题2】
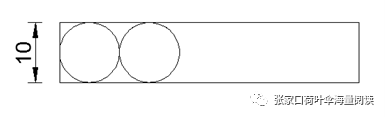
如图有一块长方形彩纸,如图彩纸的宽为10厘米,做一个圆柱体需要用多长?
【解题思路】
在图中的已知条件长方形的宽10厘米,那么圆的直径也为10厘米。
那么做一个圆柱体需要用的长度等于两个圆的直径加一个圆的周长。
公式:2d+dπ=2×10+10×3.14=31.4厘米
【例题3】
一根长2米的圆柱形木头,截去2分米的一段小圆柱后,表面积减少了12.56平方分米,那么这根木头原来的体积是多少?
【解题思路】
圆柱形木头截去一段后表面积减少了,截去一段后的圆柱形木头的上下底面积与原来木头的上下底面积是一样的,所以减少的表面积只是侧面积减少了。用减少的侧面积就可以求出圆柱的底面半径,从而求出体积。
公式:底面半径r=12.56÷3.14÷2=2分米
原木头的体积=2×2×3.14×20=251.2立方分米
【例题4】
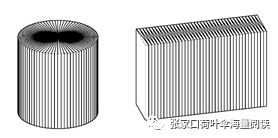
如图,把一个圆柱体切开,拼成一个与它等底等高的长方体,这个长方体的表面积比圆柱体多40平方厘米,若圆柱的底面周长是25.12厘米,圆柱的体积是多少立方厘米?
【解题思路】
圆柱体切开后拼成长方体,表面积增加了40平方厘米,增加的表面积是2个以圆柱底面半径为宽,高为长的长方形,这样就可以求出圆柱体的体积。
公式:r=25.12÷3.14÷2=4厘米
圆柱的高=40÷2÷4=5厘米
圆柱的体积=4×4×3.14×5=251.2立方厘米
【例题5】
甲乙两个圆柱体容器,底面积之比为4:3,甲容器中水的高度为7厘米,乙容器中水的高度为3厘米,再往两容器注入同样多的水,直到水的高度相等,这样甲乙两个容器的水面各上升多少厘米?
【解题思路】
甲乙两个圆柱体容器,底面积之比为4:3,注入同样多的水即水的体积相等,水面上升的高度与底面积成反比例即3:4,甲乙两个圆柱体容器中水的高度差为7-3=4厘米,哪么要使甲乙两个容器水面高度相等,甲的水面应上升4×3=12厘米,乙的水面应上升4×4=16厘米。
【例题6】
有大小两个圆柱体杯子,大杯的底面直径是6厘米,装水的高度为15厘米,小杯的底面直径是2厘米,为空杯,问从大杯往小杯倒多少水两个杯的水面高度相等?水面高度是多少?(杯子壁厚忽略不计)
【解题思路】
在大小两的杯子的水面高度相等时,水的体积与杯子的底面积成正比例,
即V大杯:V小杯=S大杯底:S小杯底=3×3×3.14:1×1×3.14=9:1
原大杯中水的体积为:3×3×3.14×15=423.9立方厘米
使两杯水面高度相等应往小杯倒水:423.9×1÷(9+1)=42.39立方厘米
两杯水面高度相等后的高度:42.39÷(1×1×3.14)=13.5厘米







